-
-
Save steveruizok/3d1bf2b95c1bbac9b46658527a2ca717 to your computer and use it in GitHub Desktop.
| export class Cache<T extends object, K> { | |
| items = new WeakMap<T, K>() | |
| get<P extends T>(item: P, cb: (item: P) => K) { | |
| if (!this.items.has(item)) { | |
| this.items.set(item, cb(item)) | |
| } | |
| return this.items.get(item)! | |
| } | |
| access(item: T) { | |
| return this.items.get(item) | |
| } | |
| set(item: T, value: K) { | |
| this.items.set(item, value) | |
| } | |
| has(item: T) { | |
| return this.items.has(item) | |
| } | |
| invalidate(item: T) { | |
| this.items.delete(item) | |
| } | |
| bust() { | |
| this.items = new WeakMap() | |
| } | |
| } |
| class Example { | |
| getOutline(shape) { | |
| const sides = 5 | |
| const ratio = 1 | |
| const cx = w / 2 | |
| const cy = h / 2 | |
| const ix = (cx * ratio) / 2 | |
| const iy = (cy * ratio) / 2 | |
| const step = PI2 / sides / 2 | |
| return Array.from(Array(sides * 2)).map((_, i) => { | |
| const theta = -TAU + i * step | |
| return new Vec2d( | |
| cx + (i % 2 ? ix : cx) * Math.cos(theta), | |
| cy + (i % 2 ? iy : cy) * Math.sin(theta) | |
| ) | |
| }) | |
| } | |
| outline(shape: T) { | |
| return outlines.get<T>(shape, (shape) => this.getOutline(shape)) | |
| } |
The other thing we can do is to pass around a single reused array at the higher level, to all these shapes' getOutlines for them to fill. This singleton array could be great for perf at very little readability cost. Let's not do that yet though.
Another thing I'd like to try is a proper array layout (e.g. [1, 2, 3, 4] or [1, 3, ...] [2, 4, ...] instead of [{x: 1, y: 2}, {x: 3, y: 4}]), after which I believe the entire cache code can go away as the function gets as fast as the caching itself =). This also means you're always hitting your worst-case getOutline scenario instead of having a cache hiding it. If your worst-case is under 16ms (now 8ms due to browsers gradually going 120fps. I'm very worried for other webapps) then you know and immediately see during usage that you don't have to optimize this again.
jesus that's clever
Just double checking, but if I know how long an array is going to be, it is always better to create an array of that length using Array(length)?
Eh I wouldn't worry about that part too much. But for your curiosity, JS arrays are C++ vectors and reallocate to double its size when they exceeds the bounds. So in the grand scheme of things maybe it doesn't matter. Again, readability first. Plus if the singleton array reuse thing we've previously discussed works out, which it might not, then this doesn't matter.
Btw the reason I can see the array reuse not working out is precisely the doubling. You'd pass around a mutable array and some shapes just bump against the array length because they have more points, in which case you have an implicitly doubling anyway sometime. Though you can further prevent that by pre-allocating an array that's long enough. Do you know of an absolute upper bound for the amount of point? There's gonna be some. At least just for testing purposes, you can try setting it to 10k or something, Your other algorithms would collapse before this limit anyway
Extracted some final code here: https://gist.github.com/steveruizok/0e4f23c7011a6ac65c9aa820d872945b
Lol that looks clean yeah. Can you benchmark it on your side to see the wins?
Also I'm suspecting the new numerical stability will help out on some edge case floating point scenarios
1 is using your code but with the Array(n) replaced with just an empty array.
2 is using your code
3 is using my original implementation with an empty array
4 is using my original implementation with Array(n)
Fastest code:
function pointsOnEllipse(cx, cy, rx, ry, n) {
const points = [];
const step = Math.PI / (n / 2);
let sin = 0;
let cos = 1;
const a = Math.cos(step);
const b = Math.sin(step);
for (let i = 0; i < n; i++) {
points[i] = { x: cx + rx * cos, y: cy + ry * sin };
const ts = b * cos + a * sin;
const tc = a * cos - b * sin;
sin = ts;
cos = tc;
}
return points;
}erp bug in the tests, one sec
Also before we try to reuse some mutable array, let's try a textbook structure-of-arrays transform. Instead of results being {x: number, y: number}[], try {x: number[], y: number[]}:
resultsX[i] = cx + (i % 2 ? ix : cx) * cos;
resultsY[i] = cy + (i % 2 ? iy : cy) * sin;
...
return {x: resultsX, y: resultsY} // or whateverThen you massage your points reading code, which hopefully is localized enough. You don't really want this structure change to spill too far, unless this also happens to be the better structure (could be).
Then you measure not this getOutline, but the iteration code over these points. I think you'll get another few times perf boost!
Your code is significantly faster (and the Array(n) makes a big improvement)
Fastest code:
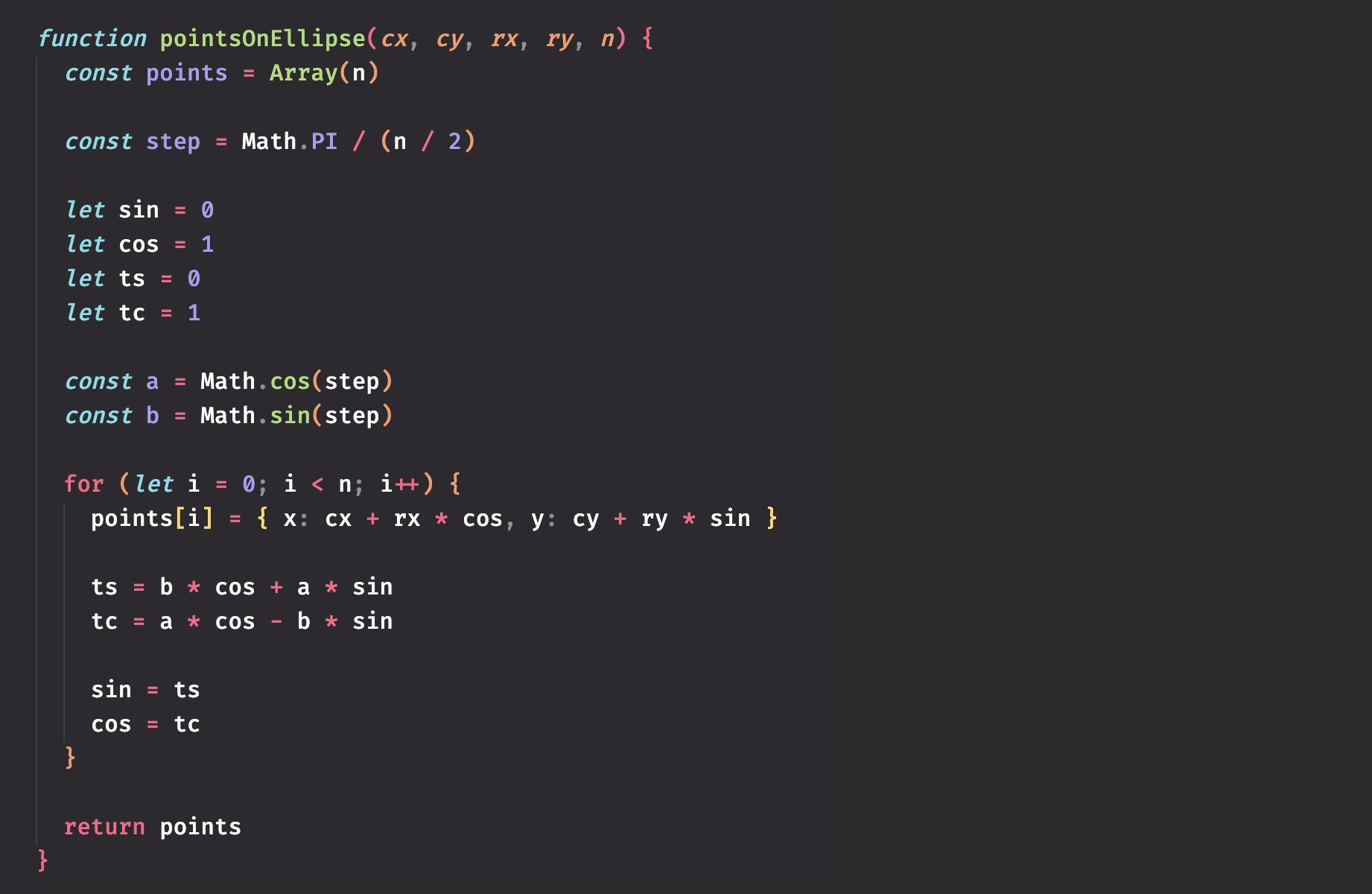
function pointsOnEllipse(cx, cy, rx, ry, n) {
const points = Array(n);
const step = Math.PI / (n / 2);
let sin = 0;
let cos = 1;
const a = Math.cos(step);
const b = Math.sin(step);
for (let i = 0; i < n; i++) {
points[i] = { x: cx + rx * cos, y: cy + ry * sin };
const ts = b * cos + a * sin;
const tc = a * cos - b * sin;
sin = ts;
cos = tc;
}
return points;
}So I see 5x boost on this hot path, numerical stability, same readability, and a better understanding of the geometry through linear algebra (debatable but yeah). We can get another 2-3x easily later through my above suggestions too. Can we remove the cache later? =)
Worth noting that 2 ternaries are gone from the loop. Those should have been cheap, but lower-level condition-less code is faster than conditional code. To be fast, remove ifs. Fewer ifs also means less debugging, win-win.
This is fun!
So here's the AoS->SoA transform. I don't have a JSBench account to share saved snippets, but you can copy the setup and the 2 tests from this gist:
https://gist.github.com/chenglou/ff603736ae48c09c9293651dc94a6adf
This isn't as big of a win than it should be (though 1/4 is pretty darn good for a hot path already given the very little readability difference). But the bigger win might be architectural: I'm wondering if you can just pass a single mutable array of ys and ys to all getOutlines, then fast iterate though xs to find the x bound, and fast iterate through ys to find the y bound. Or maybe that's not what you need.
Squeezing a little more out: https://jsbench.me/z5l819pk9w/1
The architectural change is interesting. I may be able to do that, yeah—the outline is primarily used for hit testing (ie point in polygon, or else as a series of line segment vs line segment or arc intersections), however it also used to render for certain shapes, where we pass the outline to perfect-freehand to create a path that way. The first case would just mean changing the way we do intersections (not so bad), but the second would mean creating a custom version of perfect-freehand that expects data in a certain shape.
Really though this isn't the hottest path in the app, though it is a good place to learn some of these strategies.
The points-to-svg-strings from that original tweet is much more impactful.
The matrix stuff is probably next on the block, and I've already been able to roll some of this into that!
(Since this gist's public now, here's the tweet referred to by points-to-svg-strings: https://twitter.com/_chenglou/status/1567269585585606659)
You've benchmarked creations; that SoA transform is for iteration. Here's the correct benchmark: https://jsbench.me/7gl81zd1xk/1

The memory layout rearrangement is for optimizing memory (memory is the bottleneck for modern computers, not compute). This will be especially relevant if you e.g. traverse only xs. An array of numbers is like 3x smaller than an array of objects of 2 numbers. The reason why you don't see 3x difference is because* in JavaScript everything's basically a pointer and instead of having a compact array of floats, we get an array of pointers to floats. In theory. In practice and outside of benchmarks, the JITs will do whatever.
* Well, also because in this benchmark you're accessing both xs and ys. Theoretically if you're only accessing one of the two arrays then your perf increase goes from ~25% to >30%
Tldr modern performance is mostly about shuffling your memory into the right representation*. Which is a nice endeavor because starting from data structures is important anyway.
But yes, if it's not in the hot path, then don't bother! Though there might be an argument that this is the better data layout even just for ergonomics. I wouldn't know that without trying perfect-freehand though
* again, my rough approximation is that if you're doing the sort of optimizations that increases compute at the expense of memory, by e.g. caching or whatever, then you might have already lost, especially in latency
Quick update—this is the fastest that I've gotten it so far. Surprisingly the destructuring trick is fast!
function pointsOnEllipse4(cx, cy, rx, ry, n) {
const xs = new Float32Array(n);
const ys = new Float32Array(n);
const step = Math.PI / (n / 2);
let sin = 0;
let cos = 1;
const a = Math.cos(step);
const b = Math.sin(step);
for (let i = 0; i < n; i++) {
xs[i] = cx + rx * cos;
ys[i] = cy + ry * sin;
;[sin, cos] = [b * cos + a * sin, a * cos - b * sin];
}
return { xs, ys }
}I wouldn't pay too much attention to that destructuring, which is more microbench-y really. It invokes array iterator, but here the engine clearly sees there's nothing to be invoked. Won't necessarily be true if the code shifts around. Plus, readability. Aim for simple and fast code that looks like C (this has been a solid advice for the past 20 years no matter what magic JIT has done); C doesn't have a JIT, so coding while pretending there's no JIT helps too.
Regarding Float32Array: they might be faster, but the reason is likely that they're 32-bits instead of 64-bits. So yeah here again it's about having a smaller memory footprint. But on the other hand, you've now traded off your number precision (that we just fixed) that you might need in the future. Imo this is especially relevant for SVGs (as opposed to raster graphics and 3D), since e.g. if you have 2 same shapes with different colors perfectly on top of each other, you should see a single outline, not some colors from the background shape bleeding out (aka numerical imprecision). I don't know though. Just a general observation.
The structure-of-array transform we did is fast for 2 reasons:
- Way fewer tiny allocations. Tiny objects are still relatively fast to create because they're are usually allocated around the same places ("arenas"), so, good memory locality, thus perf, and so their drawback of being more allocate-y doesn't show up as much. But when readability is the same, I try not to rely on that assumption too much and just do the predictable less allocate-y thing. Plus there's also deallocation: GC pauses etc.
- The transform makes iteration and branch predictor very happy. Iterating over a plain array of numbers is the best-case scenario for modern CPUs (and GPUs, and eh, TPUs or whatever comes next I guess. This will always be relevant).
So that's why you see that 25% perf boost at basically no cost.
One last note on your initial problem: I think if we have to cache the outlines, we should at least lift the cache to a higher level, to a single big one. Having so many little disparate caches is a bit scary.
Update: final follow-up tweet at https://twitter.com/_chenglou/status/1571430079829528577
Verify Github on Galxe. gid:YZP8XDSaNU8GruWpvhJpFZ
It's mentioned that the cache is slow. This is to be expected when using a WeakMap.
Was inverting the cache considered? Meaning storing the x,y cached properties inside each associated original shape (either as public or private fields). This ensures there is no increase in the count of objects and makes cache access super fast. I am wondering if fast caching changes the balance here.
Good point. For Steve's use-case it seems storing the entire outline array on the instance every time the shape transforms, might be viable. It does nothing for latency and uses more memory, but still, seems better than a WeakMap.




(Now that this gist is public) the goal here is to attempt to remove the caching, while properly exposing tldraw's latency problem of showing shapes' outlines, sometime when the user drags a huge selection over many shapes. Caching here only improves the throughput at the cost of worst-case latency, which isn't what we want (and is generally not what we want in a UI app since we should be modeling it as a soft real-time system, not a backend service). Though it is very appealing, since for these common actions, the shapes and their outline don't move. Still, UX-wise, we should think about what happen when many of them do move. The answer right now would be: the calculations would be even slower, since now you need to rerun
getOutlineand have a cache invalidation. The cache's also unbounded for a while. Even if we do keep the cache, it's nice to think in a direction where we can't afford it, for the sake of code simplicity (caching is one of the hardest problems) and optimization.===
Let's see if
getOutlinecan be simplified and made faster.sinandcosare both imprecise and expensive. I've turned your code into an incremental (the benign kind lol) solution using Inigo's excellent explanation at https://iquilezles.org/articles/sincos/Tldr it transforms the problem into a linear algebra one, and removes
sin&cos. So now your values are precise (check the resulting arrays and compare!). It's also 3-4 times faster now!This is slightly harder to read but mostly due to my laziness. The essence of the problem is simpler. The rest can be cleaned up.
Update: this is now cleaned up: