This article describes the Minglejingle (MJ) protocol: a redesign of Mimblewimble (MW) for non-interactive transactions. It preserves the security and privacy properties, supports payment proofs, non-interactive coinjoin and secure pruning of spent outputs.
Blockchains are distributed ledgers that preserve the transaction history so that new network participants can, at any point in the future, verify these two security properties:
- Supply security: No counterfeit coins have been created.
- Ownership security: No coins have been moved without the authorization by the owner of the associated private keys.
Bitcoin achieves unconditional supply security as a result of transparent transaction amounts. Ownership security is achieved by storing all historical transactions forever, which allows the signatures authorizing the transfer of coins to be verified at any time.
The Mimblewimble protocol, proposed in 2016 by an anonymous researcher [1], makes blockchains much more efficient, while still providing both of the security properties. MW replaces output values with homomorphic Pedersen commitments, which allows both the supply security and the ownership security to simplify to a single signature verification per transaction while removing the need to keep all historical ouputs in the blockchain.
However, the efficiency and elegance of MW comes at a cost. All transactions must be constructed interactively by the sender and all the receivers. This has both usability and security implications:
- The sender and the receivers must typically be online at the same time and be able to communicate. Since most users connected to the Internet don't have a public IP address, the interaction is usually done via Tor or using a third party service.
- The private keys are needed in order to receive funds. This means that the recipient must typically keep their private keys in a hot wallet connected to the internet. This poses an additional security risk.
There have been many proposals how to alleviate these issues and enable non-interactive/one-sided transactons in the MW protocol. However, these proposals either don't support payment proofs [2] or don't provide ownership security [3, 4, 5].
This article presents Minglejingle, a redesign of the MW protocol with the following features:
- Transactions are fully non-interactive. The sender only needs to know the recipient's address, which consists of 2 public keys.
- Addresses are not linkable to wallets.
- Transactions outputs are not linkable to addresses.
- Blocks don't link transaction inputs to outputs.
- The protocol provides both supply security and ownership security.
- Prunable data from spent outputs are not needed for chain verification.
- The protocol provides unconditional payment proofs.
As MJ represents a compromise between efficiency and usability, there are some drawbacks:
- The protocol requires more complex consensus rules than MW.
- The amount of data that new nodes need to download in order to verify the full transaction history is 2-4 times larger than in MW, depending on the fraction of spent outputs. However, this is still several times less than other non-interactive protocols with similar privacy properties (details in §7.1).
We assume that 𝔾 is a cyclic group of prime order q ≈ 22*λ, where λ is the security level in bits. Uppercase letters usually refer to group elements (public keys, commitments) and lowercase letters usually refer to numbers in Zq (scalars, private keys). We will use the additive notation for group operations.
Let G be the generator of 𝔾 and H be another element of 𝔾 with unknown discrete logarithm relationship to G.
We assume the existence of the following hash functions:
Hbis a hash function{0,1}* -> {0,1}b. For preimage resistance,b = λ. For collision resistance,b = 2*λ.Hqis a hash function{0,1}* -> Zq
These hash functions are modeled as random oracles with uniform outputs over their domains.
Tags are used to prevent the outputs of hash functions from being misused in a different context than intended. Tags will be denoted by capital letter T with a lower index specifying the name of the tag. Tags are passed to hash functions alongside other input fields. For example, Tsend is a tag specifies that the input is used in the context of sending funds.
Pedersen commitment C is an element of 𝔾 constructed as:
C = r * G + v * H
where r is the blinding factor and v is the value of the commitment. Pedersen commitments are homomorphic, which means that adding two commitments C1 and C2 to values v1 and v2 produces a commitment to (v1 + v2) mod q
When adding Pedersen commitments, their values are added modulo q. To prevent overflow, we need to restrict the possible values of v to a range much smaller than q. Range proofs are a special kind of zero-knowledge proofs that prove a commitment C is of the form r*G + v*H where 0 <= v < 2n and n is the required precision in bits, without revealing the values r or v. For monetary operations, 64-bit precision is more than enough to represent the possible range of values.
This article assumes the use of Bulletproofs++, a short and efficient range proof that requires 10 group elements and 3 scalars to prove that v is a 64-bit value. [6]. The proofs for several different commitments can be aggregated with a logarithmic increase in proof size.
If Alice owns a keypair (xa, Pa) and Bob owns a key pair (xb, Pb), then xa* Pb = xb* Pa is a secret that only Alice and Bob can compute after sharing their public keys Pa and Pb. This is called the Diffie-Helmann (DH) key exchange protocol. [7]
Schnorr signatures are a family of digital signatures based on the discrete logarithm problem (DLP). We consider 3 variants of the signature scheme with different sizes and features. All variants provide λ bits of security against forgery.
| signature | size | batch | adaptor | security proof |
|---|---|---|---|---|
| Standard Schnorr | 4*λ |
✓ | ✓ | GGM+ROM [8] |
| Short Schnorr | 3*λ |
✓ | GGM+ROM [9] | |
| Half-aggregated Schnorr | 2*λ |
✓ | AGM+ROM [10] |
-
batch = supports batch verification (several signatures can be verified with a single multiexponentiation operation)
-
adaptor = supports adaptor signatures ("scriptless scripts")
To sign a message m using the private key x (corresponding to the public key P), the signer selects a random nonce value r and calculates R = r*G. The signature then consists of the pair (R,s), where s = r + e*x with e = Hq(R, P, m).
A signature (R,s) of the message m can be verified with the public key P by checking s*G ?= R + Hq(R, P, m)*P.
To sign a message m using the private key x (corresponding to the public key P), the signer selects a random nonce value r and calculates R = r*G. The signature then consists of the pair (e,s), where s = r - e*x and e = Hλ(R, P, m).
A signature (e,s) of the message m can be verified with the public key P by checking e ?= Hλ(e*P + s*G, P, m).
Given N standard Schnorr signatures σ1 = (R1, s1), σ2 = (R2, s2), ..., σN = (RN, sN) for public key-message pairs (P1, m1), (P2, m2), ..., (PN, mN), they can be aggregated into a single signature σaggN = (R1, R2, ..., RN, sagg) of size 2*λ*(N+1) bits.
This aggregation does not require interaction with the original signers and can be done incrementally, i.e. given σaggN and a new signature σN+1, it is possible to calculate σaggN+1 (IASchnorr scheme in [10]). This has advantages for blockchain applications, allowing miners to collect transactions and incrementally aggregate them into a block.
It should be noted that the security proof for Half Schnorr requires a slightly stronger assumption (the algebraic group model) compared to Standard and Short Schnorr, which have been proven in the generic group model. However, this assumption seems sensible for practical use with elliptic-curve groups.
Standard Schnorr signatures of the same message with two or more private keys can be aggregated into one multi-signature (R,s) if the signers cooperate. This interactive protocol is described in §3.2.2 as part of the MW protocol.
For the 128-bit security level, a good choice to represent the group 𝔾 is the ed25519 elliptic curve. It is a twisted Edwards curve that has complete point addition formulas, allowing fast and secure constant-time implementations. Although this curve has a cofactor of 8, this can be eliminated by using the Ristretto abstraction for group elements, which produces a prime-order group and protects from small-subgroup attacks [11].
The table below lists the serialized sizes of the cryptographic primitives when using the ed25519 elliptic curve.
| primitive | elements | size (bytes) |
|---|---|---|
| private key, scalar | Zq |
32 |
| public key, commitment | 𝔾 |
32 |
| range proof (BP++) | 10x 𝔾, 3x Zq |
416 |
| 2x aggregated BP++ | 10x 𝔾, 5x Zq |
480 |
| Standard Schnorr | 1x 𝔾, 1x Zq |
64 |
| Short Schnorr | 1.5x Zq |
48 |
| Half-aggregated Schnorr | 1x 𝔾 |
32 |
For comparison, we show what a simplified Bitcoin protocol might look like with Confidential Transactions (CT), i.e. output amounts hidden with Pedersen commitments.
In order to spend an output, the sender must add the following data to the blockchain:
- The ID of the transaction and the index of the output that's being spent
- A Schnorr signature
(R, s)showing the possesion of the private key for the output - The difference
dbetween the blinding factors of the outputs and the blinding factors of the inputs.
If multiple inputs are spent at once, the signatures become multi-signatures (§2.6.4), so two inputs require 168 bytes of data.
The following data needs to be stored in the BCT blockchain for each output:
- The output commitment
C = r*G + v*H - A range proof showing that
0 <= v < 264 - The receiver's public key
Kr - The sender's emphemeral public key
Kefor DH key exchange - The value
vencrypted with the shared key between the sender and the receiver. The blinding factorrcan be derived deterministically from the shared secret.
If multiple outputs are created at once, the range proofs can be aggregated.
Each BCT transaction can be verified in 2 steps:
- Checking that the difference between the output commitments and the input commitments is equal to
d*G. This proves that the transaction values balance out. - Checking that
(R, s)is a valid Schnorr multi-signature with the input public keys.
The only privacy feature provided by BCT is that the transaction amounts are hidden.
Since transactions are stored on the blockchain forever, payment proofs are easy. The sender only needs to point to a transaction output and provide the private key for Ke to reveal the value of the output.
Our main baseline is the interactive MW protocol.
Each MW transaction consists of:
- One or more inputs, which are just Pedersen commitments and refer to unspent outputs of previous transactions.
- One or more outputs, each consisting of a Pedersen commitment and a range proof.
- A transaction kernel, which consists of a public key
Kand an associated Schnorr signature(R, s). - An offset
o, which can be aggregated.
If Carol, who owns an unspent output Ci = ki*G + vi*H wants to send vo coins to Dave, the following interactive protocol must be executed:
- Carol calculates the change output value
vc = vi - vo, constructs the change outputCc = kc*G + vc*H, selects a noncercand offsetoc, then sendsCi,Cc,vo,ocandRc = rc*Gto Dave. - Dave constructs his output
Co = ko*G + vo*H, constructs a range proof forCo, selects a noncerdand offsetod, calculates the kernel public keyK = Co + Cc - Ci - (oc + od)*G, calculates the aggregated nonceR = Rc + rd*Gand constructs a partial signaturesd = rd + (ko-od)*Hq(R,K), then sendsCo, the range proof,Rd = rd*G,odandsdback to Carol. - Carol completes the signature as
s = sd + rc + (kc-ki-oc)*Hq(R,K)and can finally construct the transaction consisting of the inputCi, the outputsCoandCcwith the associated range proofs, the kernelK, kernel signature(R,s)and the offseto = oc + od.
The resulting transaction can be easily validated by checking:
Co + Cc - Ci ?= K + o*Gs*G ?= R + K*Hq(R,K)
The signature verification in step 2 serves both as a balance proof (K doesn't contain any coins) and the proof of ownership.
The MW protocol allows for the removal of spent outputs and the inputs of all transactions while preserving the security properties. Each historical transaction only leaves behind the kernel, which is about 96 bytes at the 128-bit securit level.
The main points that make MW so efficient are the following:
- The use of the blinding factor to both obscure the values of the outputs and to authorize the spending.
- Unspent outputs consisting of the absolute minimum amount of data (only a commitment + range proof).
- The removal of spent outputs.
- The kernel signature being an aggregated signature over all of the involved private keys.
MW is more private than BCT. Since transaction inputs and outputs are only linked indirectly via the kernel public key and the kernel signature doesn't sign any output data, MW provides "accidental" privacy by enabling non-interactive coinjoin.
The MW blockchain doesn't include any provisions for payment proofs. If the Carol requires a payment proof, it must be provided by Dave in step 2 of the interactive protocol. The validity of the payment proof must be bound to the existence of the transaction kernel on the blockchain to resolve disputes in the case Carol doesn't complete step 3 or if Dave spends the output.
The main design goals are the following:
- Fully non-interactive transactions.
- Both supply security and ownership security .
- Unconditional payment proofs.
- Privacy equivalent to the interactive MW protocol.
- Smallest possible blockchain.
- Fastest possible verification.
For Carol to be able to construct a MW-like transaction non-interactively, she must be able to derive all values from step 2 of §3.2.2 that are provided by Dave in the interactive protocol. This can be achieved using the DH key exchange. The shared DH key can be used for the following:
- Generating the blinding factor
rdfor Dave's output commitment. The blinding factor must be known to Carol to enable her to construct the required range proofs. - Encrypting the value
voand other data associated with the payment.
| Observation 1 |
|---|
| Because the blinding factor is known by both Carol and Dave, it is no longer sufficient as a proof of ownership of the output. |
In order to restrict the ability to spend the output to Dave, the transaction output needs to include an output key that only Dave knows the private key for.
Since the blinding factors cannot be used to prove output ownership, we can safely drop the kernel commitment K from the balance verification equation §3.2.3.1, which then becomes simply:
Co + Cc - Ci ?= o$*G
This proves that no new coins were created in the transaction and it doesn't require a signature. The offset o$ ensures that coinjoins cannot be undone. This also means that MJ doesn't have transaction kernels and transaction balances are verified the same way as for Bitcoin with CT.
To enable non-interactive transactions, we need to introduce addresses. For privacy reasons, Dave's output received from Carol should be bound to a unique one-time public key that is cryptographically unlinkable to Dave's public address.
Additionally, we want to enable Dave to generate a virtually unlimited number of different unlinkable addresses so that noone can trace his online activities.
We can achieve both of these properties with a variant of the subaddress scheme used by Monero. [12]
Dave can generate a pair of private keys a and b (in practice, both keys can be derived from the same secret seed). a is called the private view key and can be used to recognize payments. b is the private spend key and is needed to spend outputs. Separating the viewing and spending ability allows the private view key to be revealed to an auditor without risking a loss of funds.
Whenever Dave needs an address, he can select an integer index i and generate the associated public address (Ai, Bi) as:
mi = Hq(Taddr, a, i)
Ai = a*(mi + b)*G
Bi = (mi + b)*G
Notice that Ai = a*Bi for any index i. This allows Dave to calculate a DH shared secret using the same private key a for all his addresses.
Carol can construct a shared secret with Dave based on his public address (A, B) constructed according to §4.4.1 for some index i unknown to Carol.
- Carol can generate a random scalar
s. - The secret shared between Carol and Dave is
Q = s*A = s*a*(mi + b)*G. - Carol will include the ephemeral public key
Ke = s*Bwith the transaction data. - Dave can derive the shared secret using his private key
aasQ = a*Ke = a*s*(mi + b)*G.
Using the shared secret Q, Carol can derive a private key x, which will allow her to construct a unique one-time public key for Dave: Ko = x*G + B. Only Dave knows the corresponding private key.
Dave can later recognize the key by calculating B = Ko - x*G.
To make it faster for Dave to recognize that a particular output key Ko is his, Carol can include a 1-byte value t = H8(Ttag, Q) with the transaction data. This will allow Dave to eliminate 99.6% (=255/256) of non-owned outputs after deriving the shared secret. This idea was first proposed for Monero and can reduce the time to test output ownership by at least 15% [13].
To achieve an efficient blockchain, we'd like to prune spent outputs. However, since we don't have transaction kernels, we need to retain some other witness data for each spent output so that:
- Ownership security can be retrospectively verified.
- A payment proof can be provided even after the recipient spends the output.
| Observation 2 |
|---|
For each spent output, the output key Ko and the associated signature must be kept in the blockchain forever. |
It would be nice to save blockchain space and include just one multi-signature for all the spent output keys in each transaction. Unfortunately, this is not possible to do securely without explicitly linking inputs together (and thus revealing common input ownership). Since any of the Ko values may be rogue keys, the keys and signatures would have to be aggregated in a way that commits to all of the keys in advance. The reader should refer to the Bellare-Neven multisignature scheme for details [14]. Note that MW doesn't have this problem because the range proofs show that none of the output commitments is a rogue key, but this cannot be done non-interactively.
The best we can do is to keep Ko and a half-aggregated Schnorr signature separately for each transaction input.
However, this still has 2 problems:
- What message should the inputs sign? We cannot sign the outputs, since that would create an explicit link we want to avoid. If we sign a message independent of the outputs, this makes the transaction malleable and any malicious network participant can swap the transaction outputs for their own.
- How can future verifiers be convinced that the key
Koin the list of spent outputs is indeed the key that was in the pruned output?
This leads to the following observations:
| Observation 3 |
|---|
The signatures with the input keys Ko must be cryptographically bound to the newly created outputs. |
The solution is two-fold:
- The sender must sign each output with an ad-hoc key
ksand includeKs = ks*Gwith the output data. This ensures that the output data cannot be tampered with. - If the nonce of the half-Schnorr signature of a transaction input is
Ro, the sender must provide a scalaro#such that:ΣTXIN Ro + ΣTXOUT Ks = o#*G. This homomorphically binds the inputs to the outputs in a similar way to MW.
| Observation 4 |
|---|
To enable pruning, the signatures with the input keys Ko must be verifiable without access to the pruned data. |
The way to solve this problem is to split the output data into two parts: unprunable data to be kept in the blockchain forever and prunable data not needed for future verification. The prunable data will be linked to the output by a signed hash.
Each MJ transaction output consists of prunable data (PD) and unprunable data (UD).
The prunable data has fields that are no longer needed if the output is spent:
| field | description | size |
|---|---|---|
Co |
amount commitment | 32 |
RP |
range proof for Co |
416 |
Ke |
key exchange public key | 32 |
t |
view tag | 1 |
v |
amount | 0/8 (hidden in the range proof) |
n |
nonce | 0/16 (hidden in the range proof) |
| total | 481 |
The unprunable data has fields necessary for future blockchain verifiers:
| field | description | size |
|---|---|---|
Ks |
sender public key | 32 |
PID |
prunable ID | 16 |
Ko |
one-time output key | 32 |
σs |
short Schnorr signature | 48 |
| total | 128 |
The total size of each output is 609 bytes.
Let's suppose that Carol and Dave have agreed in advance on an amount v to be sent and Dave has provided his public address (A, B).
- Carol can begin constructing the output for Dave by selecting a 128-bit nonce
nuniformly at random. We will later explain how this nonce can be used for payment proof. - Carol calculates a unique sending key
s = Hq(Tsend, A, B, v, n) - Carol calculates the DH exchange public key as
Ke = s*B. - Carol derives a DH shared secret as
Q = s*A. - Carol calculates the view-tag
t = H8(Ttag, Q). - Carol derives a shared secret key
u = H256(Tderive, Q) - Carol feeds the shared key
uinto a stream cipher to derive a key extensionx, a blinding factorcand the secret scalars needed for the range proof. - Carol constructs a one-time public key for Dave:
Ko = x*G + B. - Carol calculates the amount commitment
Co = c*G + v*H. - Carol constructs a range proof
RPforCoin such a way that Dave can later replay the proof to recover the output amountvand the noncenfrom the proof data. - Carol calculates
PID = H128(Tprunable, PD) - Carol generates a private key
ksuniformly at random and derives a unique sender public keyKs = ks*G. - Carol signs the tuple
(PID, Ko)using her private keyks. The result is a short Schnorr signature(es, ss).
Dave can do the following for each unspent output in the blockchain:
- Derive the nominal shared secret
Q' = a*Ke. - Derive the nominal view tag
t' = H8(Ttag, Q') - If
t != t', this output is not owned by Dave. - Derive a shared key
u = H256(Tderive, Q). - Dave feeds the shared key
uinto a stream cipher to derive a key extensionx, a blinding factorcand the secret scalars needed for the range proof. - Calculate the nominal spend key
B = Ko - x*G - If
Bis not equal to any of Dave's generated spend keys, this output is not his. - Replay the range proof to recover the amount
vand noncen. - Check that
Co ?= c*G + v*H - Look up the public view key
Aassociated withB. - Calculate Carol's sending key:
s = Hq(Tsend, A, B, v, n) - Check that
s*B ?= Ke
Note that none of these steps requires the private spend key b, so they can be done by an auditor on behalf of Dave. 99.6% of non-owned outputs will abort early in step 3 thanks to the view tag. Steps 11-12 are needed in order to prevent the Janus attack that can be used to link addresses that have the same private view key [15]. If the final check fails, Dave should not confirm the receipt of the payment and should not spend the output.
Each transaction input consists of the following two fields:
| field | description | size |
|---|---|---|
OID |
previous output ID | 32 |
Ro |
Half-aggregated Schnorr signature | 32 |
| total | 64 |
To spend a previously received output with an output key Ko, Dave must provide OID = H256(Toutput, UD) as the ID of the output being spent and a signature (Ro, so) of the empty string that can be verified with Ko, i.e.:
- Generating a random nonce
roand calculatingRo = ro*G - Calculating a challenge
e = Hq(Tschnorr, Ro, Ko) - Calculating
so = ro + e * ko
We can notice that besides authenticating Dave as the legitimate owner of the spent output, each input signature also implies that Dave knows the private key of Ro.
The signature field so can be aggregated by miners for all inputs spent in the block (see §2.6.3).
After constructing one or more outputs according to §5.1.1, Dave can complete the transaction by calculating the two transaction offsets:
o$ = ΣTXOUT cj - ΣTXIN cj
o# = ΣTXIN roj + ΣTXOUT ksj
Here TXIN is a sum over the transaction inputs, TXOUT the sum over the transaction outputs, c are the amount blinding factors, ro the input signature nonces and ks the sender private keys.
When two or more transactions are non-interactively aggregated, the offsets o$ and o# are added together and it's no longer possible to reverse the aggregation to find out which inputs belong to which outputs.
An MJ transaction consists of:
- One or more inputs. The input format is described in §5.2.
- One or more outputs. The output format is described in §5.1.
- Two offsets
o$ando#described in §5.3. - The values of
sofor each input.
The scalars o$, o# and so can be aggregated for the whole block, so the size of a 2-in 2-out transaction is 1346 bytes. A spent transaction will leave 384 bytes in the blockchain (64 bytes per input and 128 bytes per output).
In order to verify the whole transaction history, a node needs:
- All block headers.
- The total money supply
μ. This can be implicit from the block height or derived from the block headers. - The list of all input tuples
(OID, Ro). - The list of all unprunable output tuples
(Ks, PID, Ko, σs). - Prunable data of all unspent outputs.
Compared to Bitcoin, prunable data is not needed for validation.
The six validation rules are the following:
- The aggregated signature
soaggin each block is valid for all the spent inputs in that block. - The signatures
σsare valid for all outputs. - The supply balance holds:
ΣUTXO Coj ?= μ*H + o$*G - The input-output balance holds:
ΣTXIN Roj + ΣTXOUT Ksj ?= o#*G - All unspent outputs have valid range proofs.
- The
PIDof all unspent outputs matches the prunable data.
Similar rules apply for mempool transaction validation except the input signatures are not aggregated yet and the μ*H term is replaced with the sum of the spent input commitments ΣTXIN Coj.
To prove that she sent money to Dave, Carol can provide an arbiter with:
- Dave's address
(A, B) - The transaction amount
v - The one-time nonce
n
The arbiter can verify Carol's claim by:
- Calculating the sending key
s = Hq(Tsend, A, B, v, n) - Deriving the shared secret
u = H256(Tderive, s*A). - Deriving the key extension
xfromu. - Constructing the corresponding one-time public key for Dave:
Ko = x*G + B
The arbiter can then check if an input or an output exists in the blockchain with the key Ko.
If a spent input exists with this key, the arbiter is convinced that the payment has taken place. Dave's signature with the key Ko indisputably proves that Carol's output was correctly formed.
If an unspent output exists with the output key Ko, additional checks are needed to ensure that the prunable data is correctly formed. The arbiter can follow the output construction procedure from §5.1.1 and validate the output. If the output is malformed (e.g. the amount commitment doesn't have the correct value, the view tag or the hidden nonce are invalid etc.), blame can be assigned to Carol.
Given two addresses (Ai, Bi), (Aj, Bj) generated according to §4.4.1, deciding whether they belong to the same wallet requires solving the decisional Diffie-Hellman problem in 𝔾 [16]. This problem is considered intractable if the used elliptic curve has a large embedding degree, as is the case for most non-pairing-friendly curves such as ed25519.
An active attack may be attempted by Mallory if she suspects that (Ai, Bi), (Aj, Bj) are both owned by Dave. This requires her to deviate from the output construction process described in §4.3.2 by calculating the shared secret as u = H256(Tderive, s*Ai), setting the key exchange public key to Ke=s*Bi and the output key to Ko = x*G + Bj. However, Mallory won't be able to provide a nonce value n that passes the check in step 12 of §5.1.2, so Dave will be able to detect this attack and won't confirm the payment to Mallory. Mallory will not be able to provide a payment proof because in fact, she created an invalid output to address (Ai, Bj).
Linking an output to an address requires either solving the discrete logarithm problem by calculating the receiver's private view key a or by guessing the sender's nonce value n (assuming the amount is known to the attacker). Both of these problems are intractable.
There are two approaches to breaking the balance equation §5.4.3:
- Calculating the discrete logarithm of the generator
H. - Creating a valid range proof for a negative value.
The first approach requires solving the DLP in 𝔾, which is intractable. The second approach is intractable if the range proof is sound.
Stealing an unspent output with N confirmations requires either forging a signature with the output key Ko or a chain reorganization at least N blocks deep (assuming the attacker is the original sender).
Stealing an unconfirmed output requires the knowledge of the private key ks, so it can only be done by the original sender (this is called a double-spend attack).
These are the same security properties that Bitcoin has.
MJ is susceptible to the following replay attack:
- Mallory sends an output
(OID1, Ko1)to Dave. - Some time later, Dave spends the output in transaction TX2.
- Mallory again sends an identical output
(OID1, Ko1)to Dave. This requires Mallory to use the same sender nonce and amount as before. - Anyone can replay the transaction TX2 to spend this output the same way Dave spent the first copy of the output.
A similar attack applies to Mimblewimble [17]. Solving this attack may not require consensus changes because Dave will be able to detect the duplicate output and won't provide any goods or services to Mallory for the payment. If Mallory tries to dispute the payment, the arbiter will clearly see the duplicate output keys in the blockchain, which can only occur in one of two cases (besides a negligible chance of a collision):
- Mallory deliberately sent the duplicate payment.
- Mallory is a victim of a longer chain of replayed transactions.
In the first case, the fault lies with Mallory. In the second case, someone else caused the replay attack, in which case Mallory actually didn't make the payment. In both cases, the arbiter may conclude that Dave is not obligated to provide any goods or services to Mallory.
Given an output key Ko in the blockchain, Mallory can try to forge a payment proof with a value of v to the address (A,B):
- If Mallory knows the private keys for
KoandB, she can forge the proof by calculatingx = ko - b, inverting the stream cipher to calculateu, calculating a hash preimage to get the shared secretQ, solving for the discrete logarithm of the Diffie-Hellman point with respect toAand finally, the last hash preimage to get the sending noncen. - If Mallory doesn't know the private key for
KoorB, forging the proof additionally requires the calculation of the discrete logarithm ofKo - B.
In both cases, forging the proof involves solving intractable problems.
The table below lists the initial blockchain download (IBD) size of MJ in comparison with other protocols at the 128-bit security level. This comparison assumes a blockchain with 750 million transactions with 2 inputs and 2 outputs each and 85 million unspent transaction outputs. For simplicity, we only count bare transaction sizes without block headers, transaction headers, explicit fees, lock times and aggregatable fields.
| protocol | 2-2 TX size | STXO size | IBD size (GB) | IBD size (visual) |
|---|---|---|---|---|
| Mimblewimble | 1056 | -480 | 110 | * |
| Bitcoin | 280 | 210 | ** |
|
| Minglejingle | 1346 | -481 | 329 | *** |
| Bitcoin with CT | 824 | 618 | ****** |
|
| Monero | 2000 | 1500 | ************** |
The following table lists the number of Schnorr signatures and BP++ range proofs (in millions) that need to be verified for full IBD validation. Note that performance-wise, a range proof verification is equivalent to about 100 signatures. Protocols are ordered in ascending order of computational requirements.
| protocol | signatures | rangeproofs | total CPU (visual) |
|---|---|---|---|
| Bitcoin | 750 | 0 | * |
| Bitcoin with CT | 750 | <851 | ********** |
| Mimblewimble | 750 | 85 | ************ |
| Minglejingle | 3000 | 85 | **************** |
| Monero | 900002 | 750 | ***************************************************...************* |
1 Range proofs are aggregated and it's only necessary to verify the range proof of transactions with at least one unspent output.
2 Assuming CLSAG with a ring size of 16 counting as 60 Schnorr signatures based on available benchmarks.
| protocol | NITX | NICJ | CT | BLINK | TLINK |
|---|---|---|---|---|---|
| Bitcoin | ✓ | ||||
| Mimblewimble | ✓ | ✓ | ✓ | ||
| Minglejingle | ✓ | ✓ | ✓ | ✓ | |
| Bitcoin with CT | ✓ | ✓ | |||
| Monero | ✓ | ✓ | ✓ | ✓ |
- NITX: non-interactive transactions
- NICJ: non-interactive coinjoin
- CT: hidden transaction amounts
- BLINK: blocks don't link inputs to outputs
- TLINK: transactions don't link inputs to outputs
[1] Mimblewimble: https://github.com/mimblewimble/docs/wiki/MimbleWimble-Origin
[2] MW one-sided transactions: https://github.com/mimblewimble/grin-rfcs/blob/a2d9f25cdccf29904ef241df5b608ca3fd16ed61/text/0000-onesided.md
[3] One-sided transactions in MW: https://github.com/DavidBurkett/lips/blob/master/lip-0004.mediawiki
[4] MW non-interactive transactions: https://eprint.iacr.org/2020/1064
[5] Tari one-sided payment: https://rfc.tari.com/RFC-0201_TariScript.html#one-sided-payment
[6] Bulletproofs++: https://eprint.iacr.org/2022/510.pdf
[7] Diffie-Hellman: https://www.cs.utexas.edu/~shmat/courses/cs380s/dh.pdf
[8] Schnorr signatures: https://eprint.iacr.org/2012/029.pdf
[9] Short Schnorr signatures: https://eprint.iacr.org/2019/1105.pdf
[10] Half-Aggregation of Schnorr Signatures: https://eprint.iacr.org/2022/222.pdf
[11] Ristretto: https://ristretto.group/what_is_ristretto.html
[12] Monero subaddresses: https://monerodocs.org/public-address/subaddress/
[13] Monero view tags: monero-project/research-lab#73
[14] Multisignatures: https://cseweb.ucsd.edu/~mihir/papers/multisignatures-ccs.pdf
[15] Janus attack: https://web.getmonero.org/2019/10/18/subaddress-janus.html
[16] Decisional Diffie-Hellman: https://en.wikipedia.org/wiki/Decisional_Diffie%E2%80%93Hellman_assumption
[17] Grin replay attack: https://forum.grin.mw/t/enforcing-that-all-kernels-are-different-at-consensus-level/7368
I don't know if bulletproofs+ supports this, but for classic bulletproofs over secp256k1, we have the ability to hide some additional data (about 31 bytes) into the bulletproof[1][2]. Perhaps you could use that to hide the amount and nonce and save these 24 bytes:
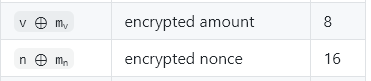
Instead of generating the nonce mask and value mask with the stream cipher, you could use the cipher to generate the secret key used to hide the bulletproof data.
[1] https://github.com/mimblewimble/secp256k1-zkp/blob/5b39fbf7f1e16e126404791923511723c4c0876d/include/secp256k1_bulletproofs.h#L181
[2] https://github.com/mimblewimble/secp256k1-zkp/blob/5b39fbf7f1e16e126404791923511723c4c0876d/include/secp256k1_bulletproofs.h#L134